Motivations
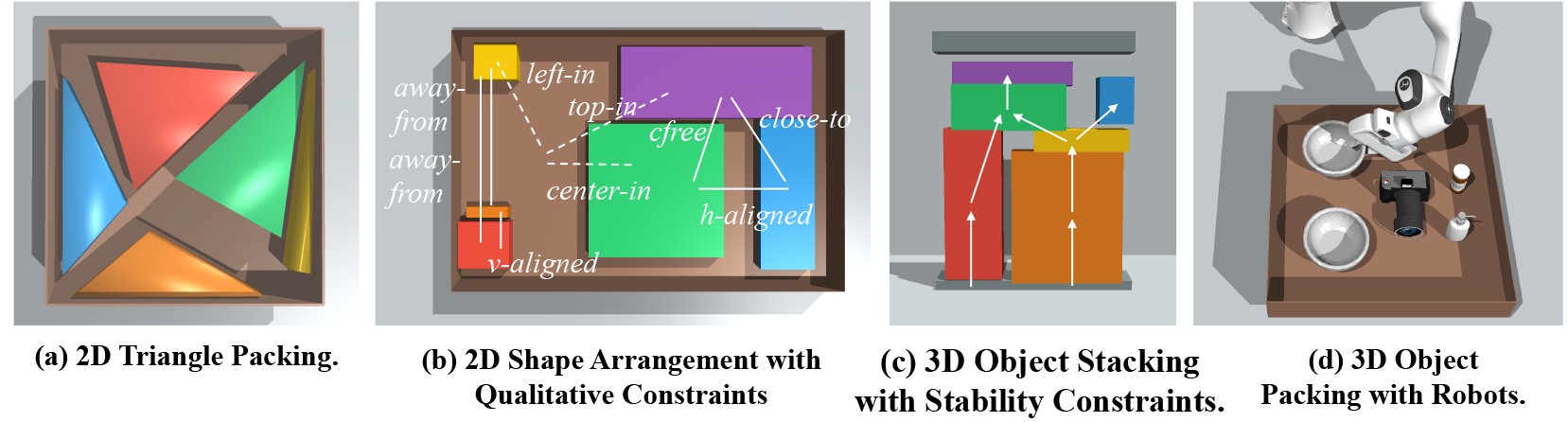
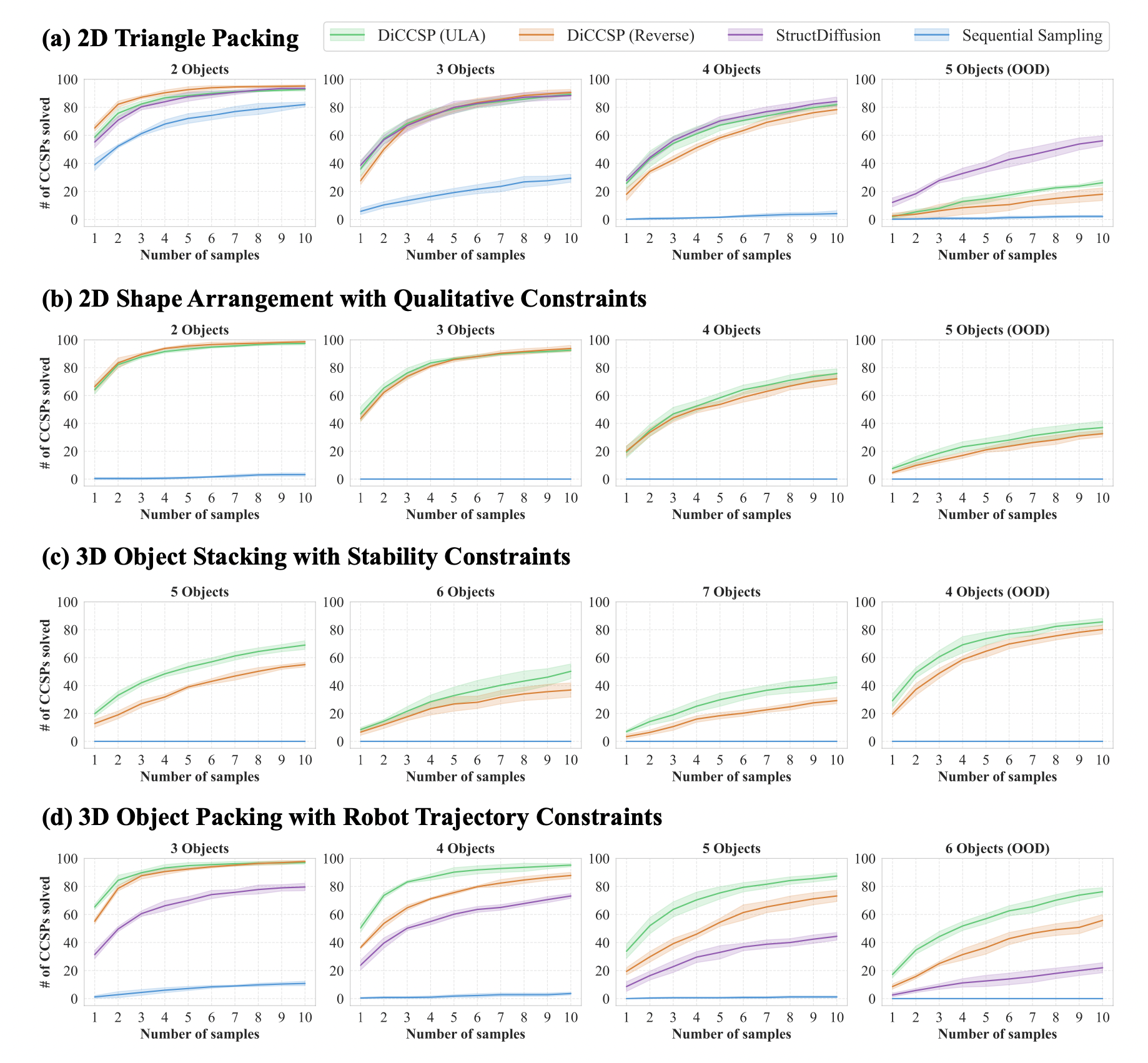
Continuous Constraint Satisfaction Problems require robot planner to conform to multiple geometric, physical, and qualitative constraints simultaneously.
For example, to place A into the tray in the figure below, we need to generate the grasping pose grasp A, placement pose pose A, and the robot arm trajectory.
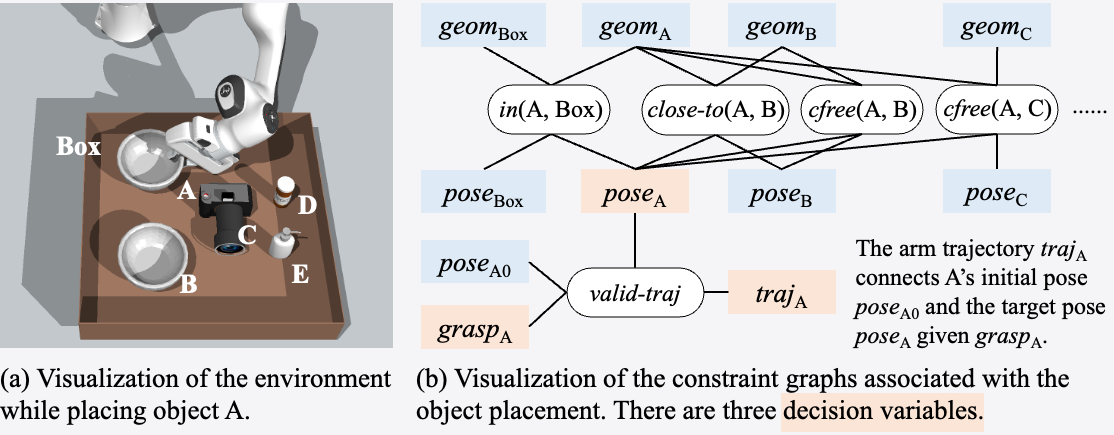
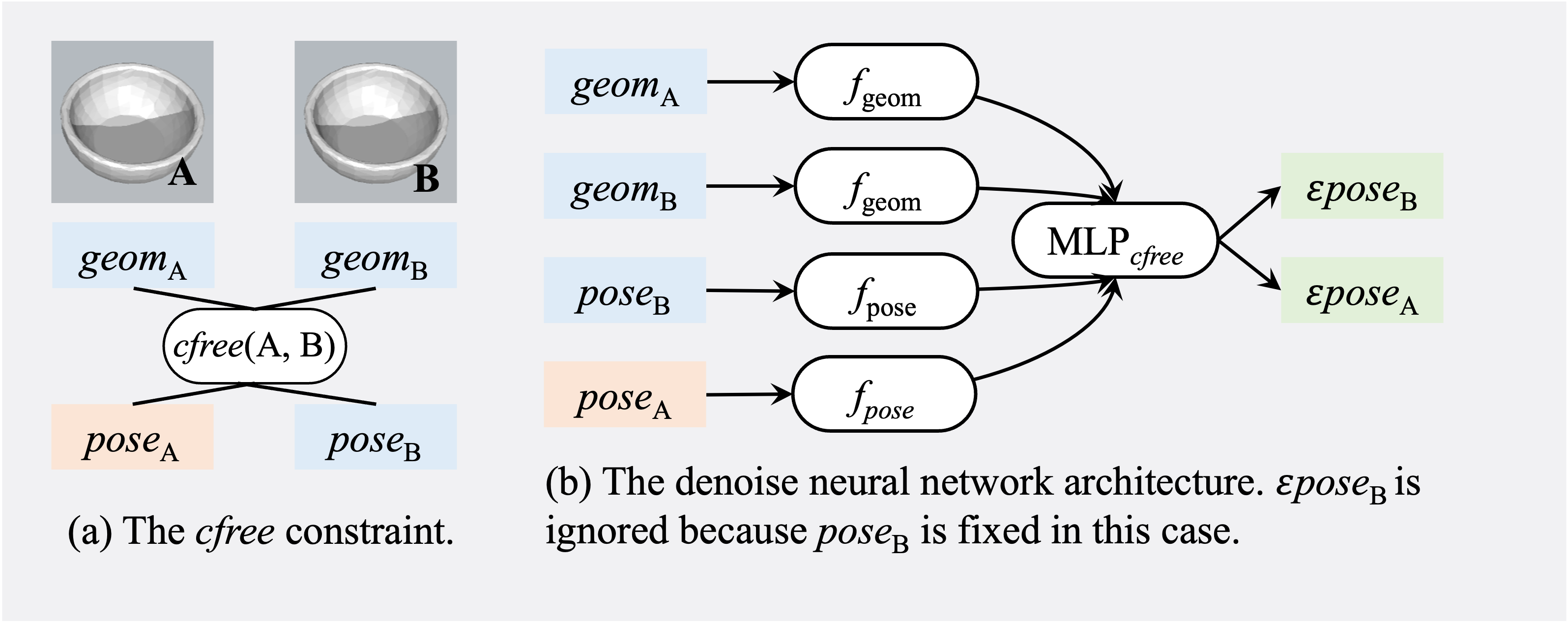
Our Diffusion-CCSP derives global solutions to CCSPs by representing them as factor graphs and combining the energies of diffusion models trained to sample for individual constraint types.